We Found a Shortcut for Quantum Chemistry Applications
Longer-lasting batteries. Life-saving drugs. High-temperature superconductors. Zero-emission fertilizers. All may be possible with quantum computing… but when?
Chemistry and materials science are among the most promising use cases for quantum computing. Intuitively, this makes sense: quantum computers get their power from the same quantum physics that governs the behavior of atoms and molecules. Quantum computers’ ability to simulate quantum physics could one day lead to the discovery of new materials for batteries, new active ingredients for pharmaceuticals, new catalysts for carbon capture — the list goes on.
But as promising as these use cases sound on paper, the reality looks a little different once you try to put these applications into practice. And we have.
In our research with bp, we discovered that quantum simulations for chemistry are still years away. The Noisy Intermediate-Scale Quantum (NISQ) devices we have today are simply not powerful enough and are too prone to error. Given these constraints, we concluded that there is no known way that NISQ devices can reliably compute many useful properties of quantum materials or molecules.
So, to bring it back to the original question, quantum chemistry applications are still years away. But our latest research has dramatically shortened that timeline.
Our Quantum Shortcut
We found a shortcut for solving two key problems in quantum chemistry applications: ground state energy estimation (GSEE) and ground state property estimation (GSPE). Estimating both the ground state energy and the ground state properties are essential steps for many practical applications where quantum computers could help discover new molecules, drugs, and materials.
Across two separate research papers, we looked under the hood of the state-of-the-art quantum methods for GSEE and GSPE and found bottlenecks that were making them infeasible on near-term quantum devices. By finding solutions to these bottlenecks, we were able to lower the barriers to running these calculations on quantum computers. We found that, for molecules relevant to battery design, our novel method for GSEE reduces the quantum circuit depth required by a factor of 78.
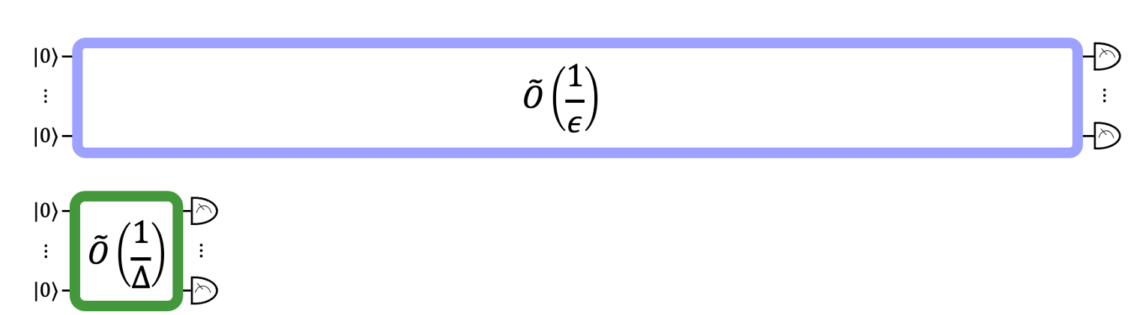
The figure above compares the relative circuit depths of the previous best GSEE algorithm (blue) with our algorithm (green).
Why do we want to reduce the circuit depth? Circuit depth refers to the number of sequential steps in a quantum circuit, or a set of instructions for a component in a quantum algorithm. The deeper the circuit, the more steps you have, and the more likely you are to experience error, particularly on error-prone NISQ devices.
The sooner we can develop quantum algorithms with low-depth quantum circuits, the sooner we can gain real value from quantum computers
One way to think about is that if p is the chance of zero error in a single operation, and L is the number of sequential operations in the circuit, the chance of avoiding error in the circuit is p^L. Thus, if p =0.999 (a one in a thousand chance of error) and L=10,000, then p^L = 0.000045 — in other words, you’re essentially guaranteed to fail. Unfortunately, the real error rates of quantum computers are much higher than one in a thousand, and quantum chemistry calculations conventionally require quantum circuits that are thousands of steps deep. So, to make these quantum chemistry calculations feasible in the near term, we need to reduce errors.
Quantum error correction is a way to reduce the error rate of each operation by using more qubits and processes. However, we anticipate there will be a limit to this reduction on early fault-tolerant quantum computers. So, we need to find other ways to reduce errors in quantum algorithms in order to run these calculations. One approach is to reduce L, the number of sequential operations needed in the algorithm. For the example above, by reducing L = 10,000 by a factor of 200, we increase the chance of zero error from 0.000045 to 0.95. This demonstrates the advantage of reducing circuit depths in quantum algorithms. Instead of waiting for improvements in quantum error correction capabilities, we can unlock quantum computations by reducing the required circuit depths.
For this reason, the research we’ve done may take years off the timeline for running these chemistry computations in the era of early fault-tolerant quantum computing. The sooner we can develop quantum algorithms with low-depth quantum circuits, the sooner we can gain real value from quantum computers in this era.
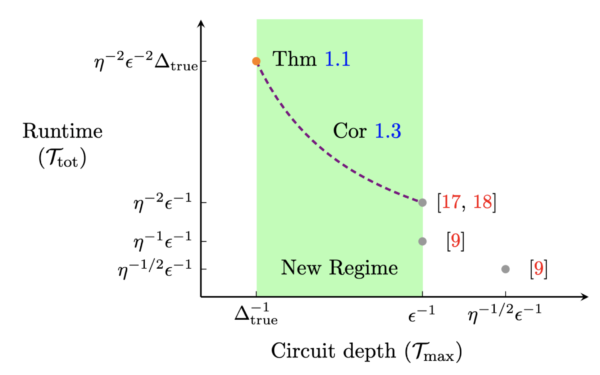
Our methods unlock quantum algorithms for GSEE with much shallower circuits. On the plot to the right, points labeled in red represent the best-known algorithms before this work, while the point labeled “Thm 1.1” and curve labeled “Cor 1.3” represents the outcome of our work. As you can see, our algorithm uses significantly shallower circuits, with the cost of longer runtimes.
Ground State Energy Estimation
The ground state energy of a molecule refers to the lowest possible energy that the state of a molecule can realize. It’s an essential value to know when comparing different molecules for a given chemistry application, and as such, it has been the focus of quantum algorithm development in chemistry. GSEE is also a key part of Zapata history: before co-founding Zapata, Alán Aspuru-Guzik pioneered the field of quantum computing for quantum chemistry and helped invent the variational quantum eigensolver (VQE), the first algorithm to solve the GSEE problem on a NISQ device.
In our recent work with bp, however, we found that it would be impractical to use VQE alone to estimate ground state energies for molecules of industrial interest using NISQ devices. Hence the need for new algorithms that can solve GSEE on near-term quantum computers.
Previous methods for GSEE, including quantum phase estimation (QPE) and more recent advances require quantum circuits for which an increase in desired accuracy costs an increase in circuit depth. This prompted us to investigate the question: is this high circuit depth cost necessary? Our research found that increased accuracy does not necessarily require deeper circuits.
In the new quantum algorithm we developed for GSEE, the circuit depth is inversely proportional to the energy gap of the molecule or material, or the energy required to promote a valence electron bound to an atom to move freely through the material and conduct an electric current. For many molecules and materials of industrial relevance — such as those used in batteries — this energy gap can be several orders of magnitude larger than the desired accuracy for GSEE. Accordingly, our algorithm would enable the circuit depth to be reduced by several orders of magnitude compared to previous GSEE algorithms.
The reduction in circuit depth lowers the barrier for implementing the algorithm on an early fault– tolerant quantum computer. While this reduction in circuit depth does require an increased number of total circuits that need to be run, we also show how to reduce this cost by increasing the circuit depth. In other words, while in the near term we may need to run more circuits at low depth, as hardware matures and we can run deeper circuits, we can also reduce the number of circuits that need to be run.
You can read the research paper on our GSEE algorithm here. The research includes important contributions from interns Ruizhe Zhang and Shuchen Zhu and Daniel Stilck-França, a quantum information researcher at ENS Lyon.
The reduction in circuit depth lowers the barrier for implementing the algorithm on an early fault- tolerant quantum computer.
Ground State Property Estimation
Estimating the ground state energy of a molecule is an important step. But for many practical applications, such as in drug or material discovery, you need to estimate properties of the ground state beyond just the energy. These include transport properties, electric dipole moments, and molecular forces. Previous research has shown that it is even harder to estimate these properties than it is to estimate the ground state energy itself.
In our other paper, published recently in Quantum Journal, we proposed a novel hybrid quantum-classical algorithm that can estimate ground state properties with high accuracy using low-depth quantum circuits. These properties include Green’s functions, which are used to predict the mobility of electrons in materials, and the one-particle reduced density matrices used to predict the polarizability of a molecule. Calculations like these are critical in the design of materials and drugs, and thus provide an opportunity for quantum computation to unlock new capabilities in these industries.
Taken together, these two research papers lay the groundwork to carry out industrially-relevant molecular and materials calculations on early fault-tolerant quantum computers.
Next Steps
Finding a shortcut to quantum advantage in chemistry is only the beginning. We still don’t know how much of a shortcut this work represents or how much closer we are to quantum advantage. For example, while we can estimate that our work reduced the circuit depth required for GSEE by a factor of 78, the field is still developing tools for predicting what time and qubit number it would take to run these computations. Will it take a day, a week, or a month to run? Will it need thousands of qubits, or millions of qubits? We don’t know yet, as it will depend on the speed of progress in quantum hardware and quantum algorithms.
Our research will continue in several directions, but one important next phase will be to create resource estimates to quantify exactly how much time and qubits will be required to run these GSPE and GSEE calculations using the shortcuts we discovered. We are currently working on a project with DARPA to develop tools for resource estimation that will be invaluable for determining when we can run our new quantum chemistry algorithms.
From there, we will have a clearer picture of when we can expect a quantum advantage in chemistry, and we can work to reduce the resource requirements even further by finding additional shortcuts. And with these shortcuts, we may be able to achieve the kinds of breakthroughs in chemistry and materials science that can change the world, whether that’s in battery design, drug discovery, or elsewhere.
Stay tuned!





